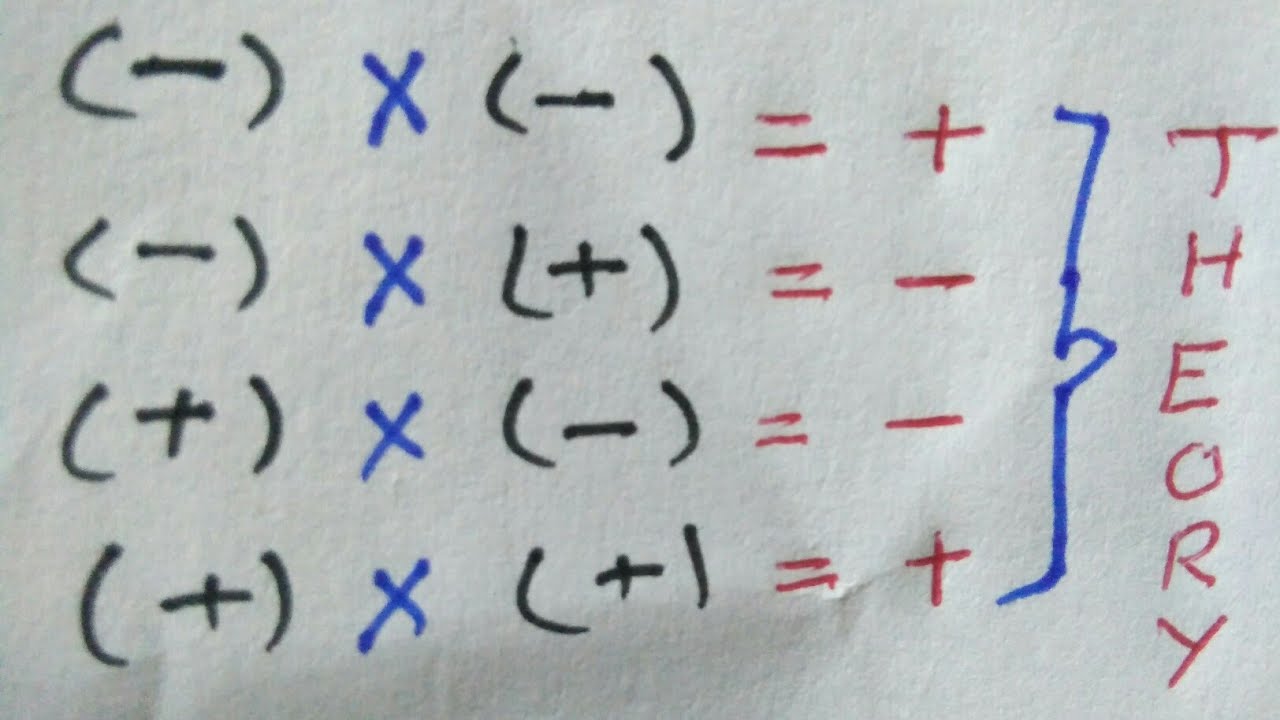Mathematics is a fascinating field that provides the foundation for various concepts in our daily lives. One of the most intriguing aspects of math is the relationship between positive and negative numbers. When we delve into the operation of multiplication, we encounter a fascinating phenomenon: the equation of positive times a negative equals. This principle, while seemingly simple, opens the door to a deeper understanding of mathematical rules and their applications. As we explore the fundamentals of this concept, it is essential to grasp not only the mechanics behind it but also the implications it holds in both mathematical theory and practical problem-solving.
In this article, we will dissect the concept of positive times a negative equals to better understand its significance in mathematics. We will cover essential principles, provide examples, and clarify common misconceptions. By the end of this exploration, readers will possess a clearer comprehension of how these operations function and their relevance in real-life situations.
Whether you are a student grappling with math homework or someone looking to refresh your knowledge, understanding the relationship between positive and negative numbers is crucial. This article aims to break down the complexities surrounding this topic and present it in a digestible format, ensuring that everyone can grasp the concept of positive times a negative equals.
What is Positive Times a Negative Equals?
The operation of multiplying a positive number by a negative number yields a consistent result: a negative number. This fundamental rule is one of the cornerstones of arithmetic and forms the basis for many mathematical applications. For example, when we multiply 3 (a positive number) by -2 (a negative number), the result is -6. This outcome is not random; it follows the established rules governing positive and negative numbers.
Why Does Positive Times a Negative Equal a Negative?
To understand why positive times a negative equals a negative, we need to delve into the properties of numbers. The concept can be illustrated through various examples and visual aids, such as number lines. When you think of multiplication as repeated addition, this principle begins to make sense. For instance, multiplying 3 by -2 can be viewed as adding -2 three times, which leads us to -6. This visualization helps solidify the understanding that the product of a positive and a negative number results in a negative outcome.
Can You Provide Examples of Positive Times a Negative Equals?
Certainly! Here are several examples to illustrate the concept of positive times a negative equals:
- 5 × -4 = -20
- 10 × -3 = -30
- 7 × -2 = -14
- 12 × -1 = -12
Each of these examples follows the rule that multiplying a positive number by a negative number results in a negative product. Such consistency is what makes mathematics reliable and predictable.
What Happens When You Multiply Two Negative Numbers?
A common question that arises is what happens when you multiply two negative numbers. The answer is quite interesting: negative times a negative equals a positive. For example, -3 × -2 = 6. This outcome may seem counterintuitive at first, but it can be explained through the rules of arithmetic and the concept of cancellation. When two negatives are multiplied, they "cancel" each other out, resulting in a positive number.
How is Positive Times a Negative Used in Real Life?
The principle of positive times a negative equals has practical applications in various fields, including finance, physics, and computer science. Here are a few scenarios:
- In finance, a positive profit multiplied by a negative growth rate can indicate a loss in profitability.
- In physics, positive velocity in a negative direction can signify movement backward.
- In computer programming, positive values may be adjusted by negative coefficients to achieve desired outcomes.
These examples illustrate how this mathematical principle extends beyond the classroom and into real-world applications.
What Are Common Misconceptions About Positive Times a Negative Equals?
Despite the straightforward nature of the rule that positive times a negative equals a negative, several misconceptions exist. Some people may mistakenly believe that multiplying a positive number by a negative number results in a positive outcome. This misunderstanding can lead to confusion in problem-solving scenarios. It is crucial to reinforce the correct interpretation of this principle to avoid errors in calculations.
How Can You Practice Positive Times a Negative Equals?
Practicing multiplication involving positive and negative numbers is essential for mastering this concept. Here are a few methods to enhance your understanding:
- Work through practice problems in math textbooks or online resources.
- Create flashcards with positive and negative numbers to reinforce the multiplication rules.
- Utilize interactive math games that focus on integer operations.
Regular practice will lead to increased confidence and proficiency in handling positive and negative multiplications.
Conclusion: Embracing the Concept of Positive Times a Negative Equals
Understanding the principle of positive times a negative equals is paramount for anyone looking to excel in mathematics. By grasping the underlying rules and practicing regularly, individuals can enhance their mathematical skills and apply these concepts to real-life scenarios. Whether you are a student or simply someone interested in mathematics, embracing this principle will provide a stronger foundation for future mathematical endeavors.
Article Recommendations
- Steamunlocked Download Cracked Games Free
- Meet Accomplished Leader Jennifer Grant
- The Ultimate Guide To Hazel Moder The Next Generation Of Hollywood Star