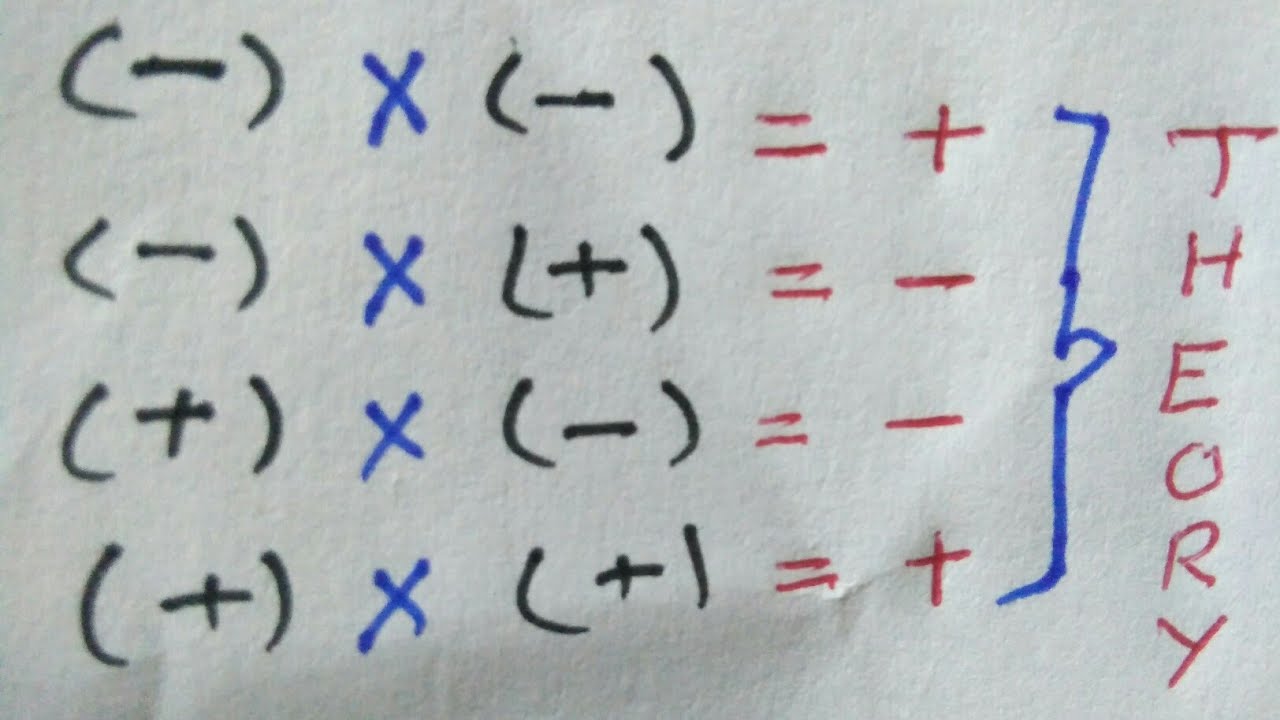Mathematics often presents us with paradoxes that challenge our intuition, and one of the most intriguing concepts is the idea of a "negative times a negative." This seemingly counterintuitive notion is foundational in mathematics, yet many people struggle to grasp why the product of two negative numbers results in a positive number. By delving into the intricacies of this concept, we can uncover the underlying principles that govern multiplication and the broader implications it has in various fields, from algebra to real-world applications.
Throughout history, mathematics has evolved, with pivotal discoveries reshaping our understanding of numbers and operations. One such discovery is the rule for multiplying negative numbers, which not only enhances our mathematical toolkit but also encourages critical thinking. The significance of "negative times a negative" extends beyond the classroom, influencing areas such as physics, economics, and even computer science. By grasping this concept, we equip ourselves with the ability to tackle complex problems and make informed decisions.
In this article, we will explore the essence of "negative times a negative," dissect its implications, and answer common questions surrounding this topic. Whether you're a student striving to master multiplication or simply curious about the logic behind it, our comprehensive guide will illuminate the path to understanding this mathematical phenomenon.
What is the Rule for Negative Times a Negative?
To fully comprehend the rule that states a negative times a negative equals a positive, we must first revisit the definitions of positive and negative numbers. Positive numbers represent quantities greater than zero, while negative numbers signify quantities less than zero. When we multiply a negative number by a positive number, the result is negative. However, when we introduce another negative number into the equation, the outcome becomes positive. This transition can be illustrated with a simple example:
- Example: -2 x -3 = 6
Why Does a Negative Times a Negative Equal a Positive?
To understand why multiplying two negative numbers yields a positive result, we can examine the concept through various lenses. One effective way to visualize this is through the use of a number line. When you multiply by a negative number, you are essentially flipping the direction on the number line. Therefore, when you multiply a negative by another negative, the direction flips twice, returning to the positive side.
Can You Provide a Real-Life Example of Negative Times a Negative?
Absolutely! Consider the context of debt. If you owe $100 (a negative amount), and you are forgiven that debt (another negative action), the outcome is a positive scenario: you now have $100 that you don't owe. This real-life example illustrates how "negative times a negative" can lead to a favorable outcome in practical situations.
How Does This Concept Apply in Algebra?
In algebra, the multiplication of negative numbers is frequently encountered in various equations and expressions. When solving equations, understanding that a negative times a negative results in a positive allows for more streamlined problem-solving. For instance, when simplifying algebraic expressions, the rule becomes essential:
- If x = -5 and y = -10, then x * y = 50
What Are Some Common Misconceptions About Negative Times a Negative?
Despite its fundamental nature, many students harbor misconceptions about "negative times a negative." Some may believe that multiplying two negative numbers should yield a negative result, as they associate negativity with undesirable outcomes. It's crucial to dispel these myths through education and practice, reinforcing the understanding that mathematical rules are grounded in logic and consistency.
How Can We Teach the Concept of Negative Times a Negative?
Teaching the idea of "negative times a negative" can be made more accessible through various strategies:
- Visual aids, such as number lines, to illustrate the concept.
- Real-world examples to connect mathematics with everyday experiences.
- Interactive activities that encourage students to explore the rules through hands-on learning.
What Are the Broader Implications of Understanding Negative Times a Negative?
Grasping the concept of "negative times a negative" has far-reaching implications beyond the confines of mathematics. In fields such as economics, understanding this principle can aid in interpreting financial data and making informed decisions. Similarly, in physics, the application of negative numbers in calculations can lead to more accurate representations of physical phenomena.
Conclusion: Embracing the Complexity of Mathematics
In conclusion, the concept of "negative times a negative" stands as a testament to the complexity and beauty of mathematics. By embracing this idea, we not only enhance our mathematical proficiency but also develop critical thinking skills that are applicable in various domains. As we continue to explore the depths of mathematics, let us remember that understanding the rules of numbers can lead to greater clarity and insight in our everyday lives.
Article Recommendations
- The Ultimate Guide To Hazel Moder The Next Generation Of Hollywood Star
- The Definitive Guide To Judd Nelson Exploring The Life And Legacy Of A Hollywood Icon
- Billionaire In The Making The Rise Of Kathy May Fritz