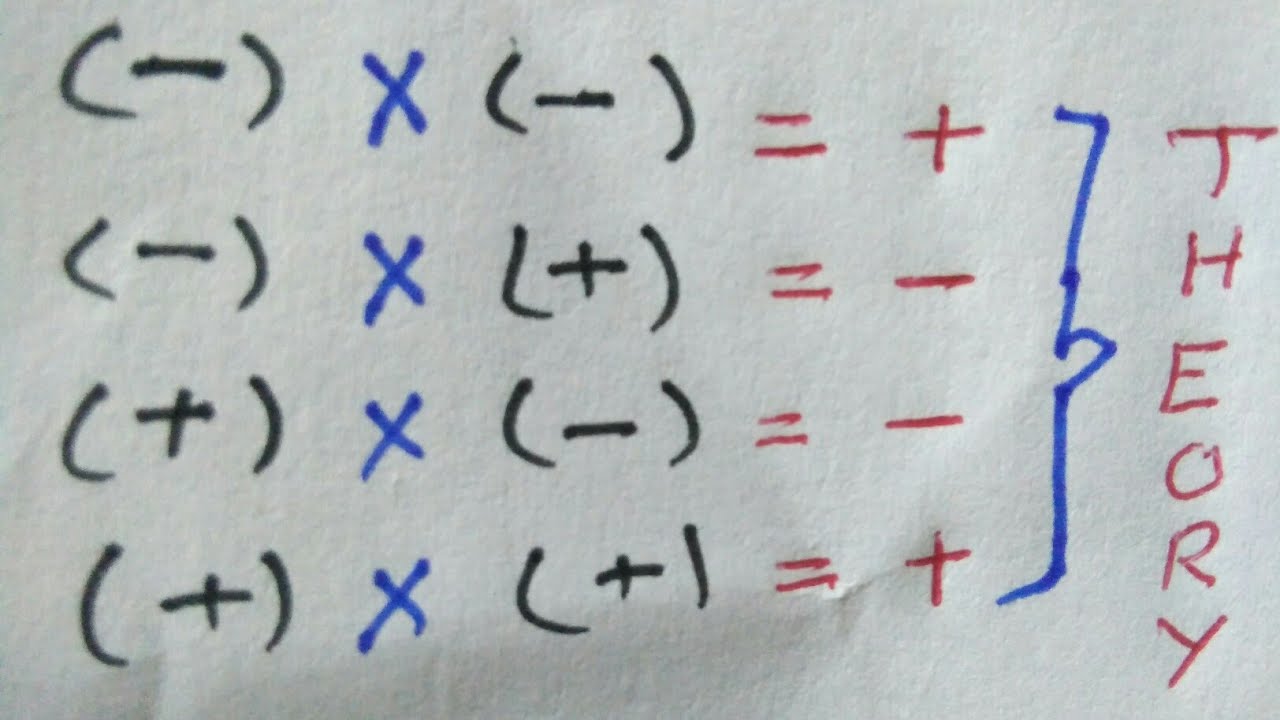The world of mathematics often presents intriguing concepts that can sometimes be confusing. One such concept is the multiplication of negative numbers, specifically the idea of "neg times neg." This phrase refers to the multiplication of two negative integers, which yields a positive result. The reasoning behind this may seem counterintuitive at first, especially for those new to the rules of multiplication. However, understanding the rationale behind this principle is crucial for mastering basic algebra and arithmetic.
When we delve into the realm of negative numbers, we discover a unique set of rules that govern their behavior. The multiplication of negative integers is not merely a random occurrence but follows a consistent pattern dictated by mathematical principles. To grasp this concept fully, it is essential to explore why multiplying two negatives results in a positive outcome and how this understanding applies to various mathematical operations.
As we explore the idea of neg times neg, we will also touch upon its practical applications in everyday life and advanced mathematics. By breaking down the principles at play, we can demystify this topic and provide a clear understanding of why "neg times neg" holds true. So, let's embark on this mathematical journey to unravel the mysteries of negative numbers and their interactions.
What is the Rule for Neg Times Neg?
To understand the rule for neg times neg, we must first consider the basic multiplication principles. When we multiply two numbers, we are essentially adding one number to itself a certain number of times, depending on the value of the other number. But what happens when both numbers are negative?
Why Does Neg Times Neg Equal Positive?
At first glance, it may appear illogical that multiplying two negative numbers results in a positive number. However, this outcome can be explained through several perspectives:
- **Number Line Concept**: When you move left on a number line, you're subtracting, which represents a negative number. Moving left again (another negative) brings you back to the right, resulting in a positive number.
- **Pattern Recognition**: If we observe the multiplication patterns of positive and negative numbers, we can conclude that neg times neg must yield a positive result to maintain consistency in the mathematical system.
- **Real-World Analogy**: Consider debt as a negative value. If you owe money (a negative), and you eliminate that debt (another negative), you gain financially, resulting in a positive outcome.
How Can Neg Times Neg Be Illustrated?
To illustrate the concept of neg times neg, we can use simple numerical examples:
- -2 x -3 = 6
- -5 x -4 = 20
- -7 x -1 = 7
In each of these examples, the product of two negative numbers yields a positive result, reinforcing the fundamental rule of neg times neg.
What Are Some Practical Applications of Neg Times Neg?
The concept of neg times neg is not merely an abstract mathematical principle; it has real-world applications as well. Here are a few domains where this rule plays a crucial role:
- **Finance**: Understanding debt and profit calculations often involves negative and positive values, making the concept of neg times neg essential.
- **Physics**: In physics, negative values might represent direction (e.g., velocity), and understanding how these interact can lead to accurate calculations of motion.
- **Computer Science**: Algorithms and programming often utilize mathematical principles, including neg times neg, to solve problems effectively.
How Do Students Typically Learn About Neg Times Neg?
Students encounter the concept of neg times neg in various educational settings, often beginning in elementary school. The teaching methods may include:
- **Visual Aids**: Teachers often use number lines and graphs to demonstrate how negative numbers interact.
- **Interactive Activities**: Engaging students through games or practical exercises can help solidify their understanding of neg times neg.
- **Real-Life Examples**: Relating mathematical concepts to everyday situations can make the learning process more relevant and easier to comprehend.
Is There Any Controversy Surrounding Neg Times Neg?
While the rule of neg times neg is widely accepted, some individuals may still struggle to grasp the concept. Debates may arise in educational settings, where students question the logic behind the result. It is essential for educators to provide clear explanations and address any misconceptions to foster a stronger understanding of negative numbers.
Conclusion: Embracing the Concept of Neg Times Neg
In summary, the concept of neg times neg is a fundamental principle of mathematics that illustrates how two negative numbers can yield a positive product. By examining the reasoning behind this rule, students and enthusiasts can develop a deeper understanding of negative numbers and their applications in various fields. Whether in finance, physics, or everyday life, recognizing the importance of neg times neg can enhance one's mathematical literacy and problem-solving skills.
Article Recommendations
- The Ultimate Guide To Leslie Easterbrook A Hollywood Icon
- The Ultimate Guide To Seann William Scott From Stifler To A Star
- The Marvelous World Of Andrew Stevens