When it comes to sorting algorithms, the efficiency of a method is often a primary concern for developers and computer scientists alike. Among various sorting techniques, Shell Sort stands out for its ability to handle large datasets with varying degrees of complexity. However, understanding the space complexity of Shell Sort is crucial for optimizing performance and ensuring effective resource utilization. In this article, we will delve into the nuances of Shell Sort space complexity, exploring its implications and practical applications.
Shell Sort, invented by Donald Shell in 1959, is an extension of insertion sort that allows the exchange of items that are far apart. The algorithm uses a gap sequence to determine which elements to compare and sort. This unique approach significantly enhances the performance of traditional insertion sort, especially for larger datasets. Yet, while the time complexity of Shell Sort has been widely discussed, the space complexity is equally important to understand, particularly for applications where memory usage is a critical factor.
As we explore the intricacies of Shell Sort space complexity, we aim to address several pertinent questions regarding its efficiency and practical implications. By dissecting the algorithm's mechanics and analyzing its performance in real-world scenarios, we can draw insightful conclusions that will benefit both novice and experienced programmers. In this article, we will answer common questions about Shell Sort space complexity and provide clarity on its role in the larger context of sorting algorithms.
What is Shell Sort Space Complexity?
Shell Sort space complexity refers to the amount of additional memory required by the algorithm to perform its sorting operations. Unlike some sorting algorithms that require substantial additional space, Shell Sort is primarily an in-place sorting algorithm, meaning it sorts the elements within the array without needing significant extra memory. The space complexity can be classified as follows:
- **Auxiliary Space**: Shell Sort typically requires O(1) auxiliary space, as it primarily uses a constant amount of extra space for variables and temporary storage during sorting operations.
- **Input Space**: The input space is O(n), as it needs to store the elements of the array being sorted.
Why is Shell Sort Considered an In-Place Sorting Algorithm?
Shell Sort is deemed an in-place sorting algorithm due to its minimal additional memory requirements. It operates directly on the list to be sorted, making it efficient in terms of space. This is in contrast to algorithms like mergesort, which require additional memory proportional to the size of the input. The in-place nature of Shell Sort allows it to be more suitable for environments with limited memory resources.
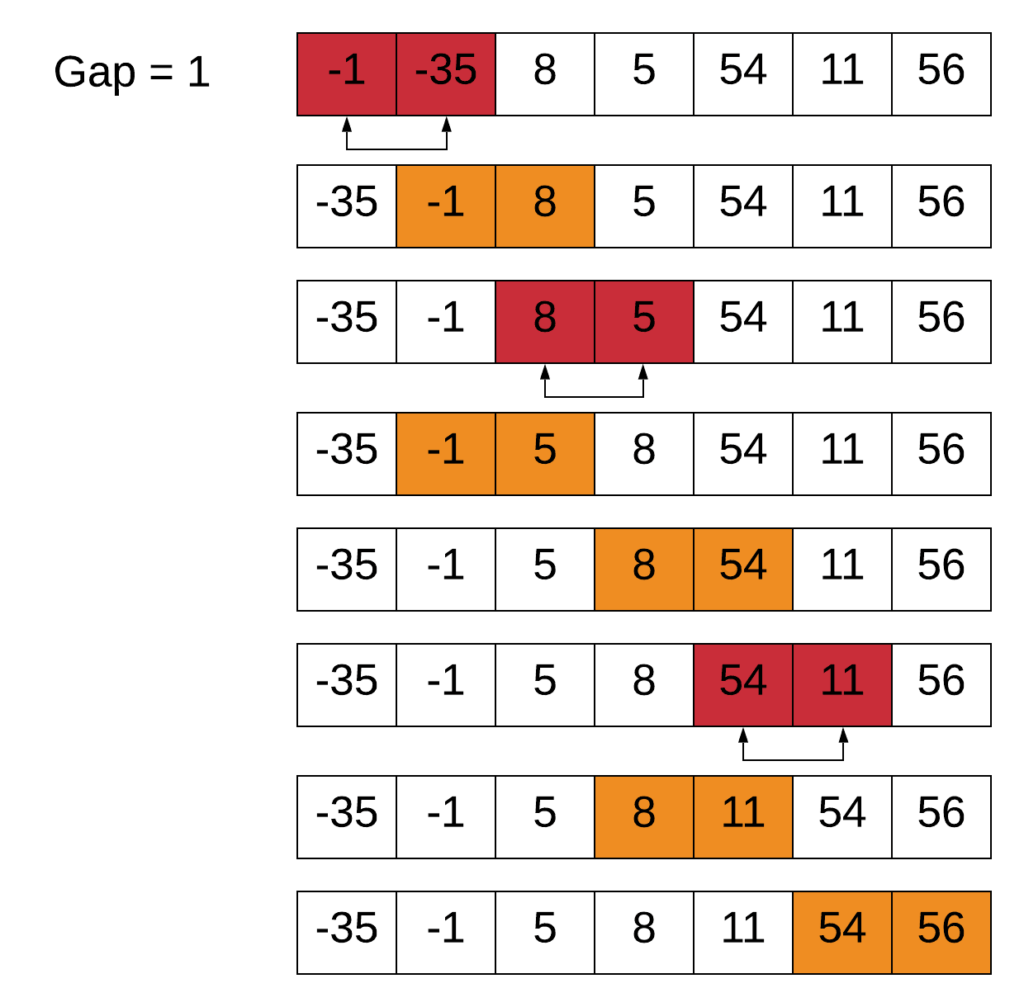
How Does the Gap Sequence Affect Shell Sort Space Complexity?
The gap sequence in Shell Sort is critical as it determines which elements are compared and sorted. Various sequences can be used, including the original sequence proposed by Donald Shell and more refined sequences that improve performance. While the choice of gap sequence affects the time complexity of the algorithm, it does not significantly impact space complexity. Regardless of the gap sequence, Shell Sort maintains its O(1) auxiliary space requirement.
What are the Advantages of Shell Sort Space Complexity?
Understanding the advantages of Shell Sort space complexity can illuminate why this algorithm is preferred in certain scenarios. Some benefits include:
- **Memory Efficiency**: With a space complexity of O(1), Shell Sort is ideal for systems with restricted memory availability.
- **Performance on Large Datasets**: Shell Sort can handle larger datasets more effectively than many other in-place sorting algorithms, thanks to its gap sequence approach.
- **Simplicity**: The algorithm's straightforward implementation and low memory overhead make it an attractive choice for many applications.
What are the Limitations of Shell Sort Space Complexity?
While Shell Sort has several advantages, it is not without limitations. Among these are:
- **Non-Optimal for Very Large Datasets**: Although Shell Sort is efficient for moderate-sized datasets, it may not be the best choice for extremely large datasets when compared to more advanced algorithms like quicksort or heapsort.
- **Gap Sequence Dependency**: The performance of Shell Sort heavily relies on the selected gap sequence, and suboptimal sequences can lead to inefficient sorting times.
How Can Developers Optimize Shell Sort Space Complexity?
Developers can optimize Shell Sort space complexity through several strategies:
- **Choose Efficient Gap Sequences**: Utilizing known effective gap sequences can improve the algorithm's performance without compromising space efficiency.
- **Limit Data Movement**: Minimizing the number of moves and swaps can help conserve memory and reduce overhead during sorting.
Conclusion: Why Understanding Shell Sort Space Complexity Matters?
In conclusion, understanding Shell Sort space complexity is essential for developers aiming to create efficient sorting solutions. Its O(1) auxiliary space requirement makes it a practical choice in memory-constrained environments, while its adaptability for different gap sequences allows for improved performance on various datasets. As we continue to evolve in the field of computing, comprehending the nuances of sorting algorithms like Shell Sort will remain a cornerstone of effective software development.
Article Recommendations
- Vegamoviestoo The Ultimate Movie Streaming Destination
- The Ultimate Goojara Movies Experience Explore A World Of Entertainment
- Meet Accomplished Leader Jennifer Grant

![[Solved] Time complexity for Shell sort? 9to5Answer](https://i2.wp.com/sgp1.digitaloceanspaces.com/ffh-space-01/9to5answer/uploads/post/avatar/791165/template_time-complexity-for-shell-sort20220722-3738824-6uvsdf.jpg)