In the world of mathematics and science, precision is paramount, and this is where the concept of significant figures comes into play. Adding significant figures may seem like a daunting task for many, especially for students venturing into the realms of physics, chemistry, or advanced mathematics. However, understanding how to properly add significant figures is essential not only for academic success but also for real-world applications where accuracy is a must. This guide aims to demystify the process of adding significant figures, ensuring that you can approach your calculations with confidence.
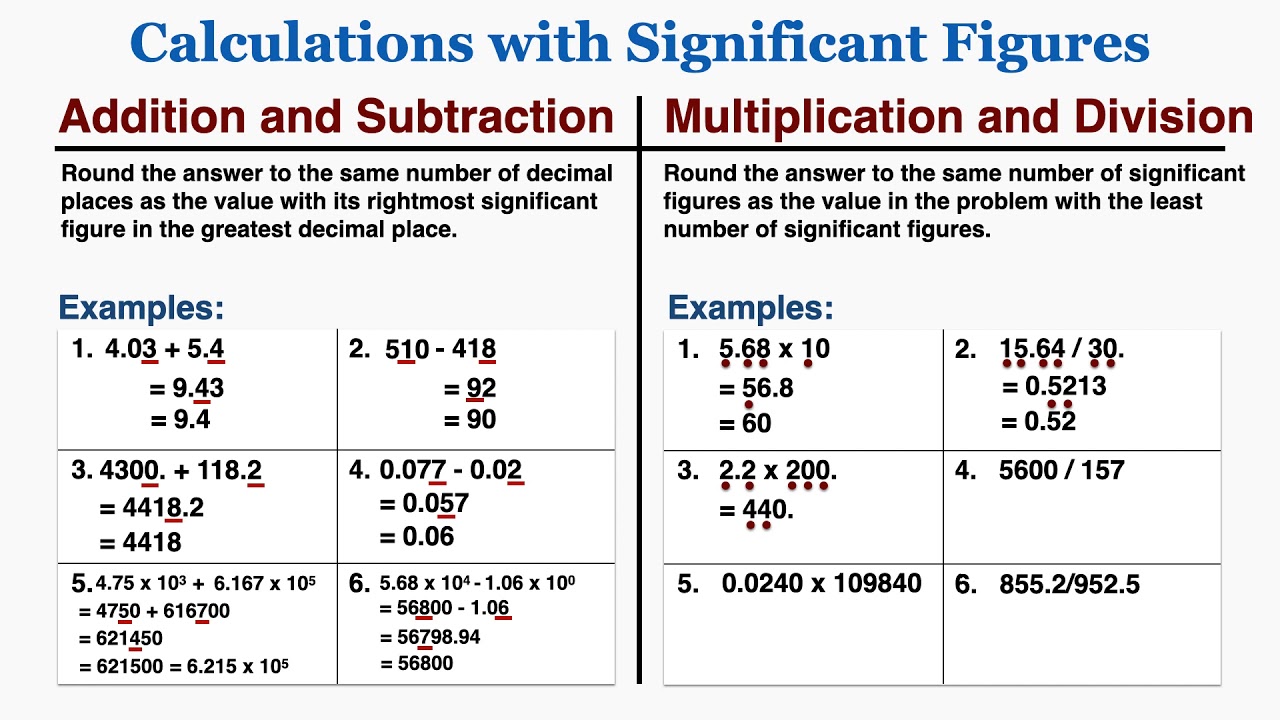
Significant figures are the digits in a number that contribute to its precision. These include all non-zero digits, any zeros between significant digits, and trailing zeros in the decimal portion. When it comes to addition and subtraction, the rule of thumb is that the result should be reported with the same number of decimal places as the number with the least decimal places in the original calculation. This principle of precision helps in maintaining the integrity of data, especially in scientific experiments where even minor discrepancies can lead to vastly different outcomes.
As we delve deeper into the topic of adding significant figures, we will explore various aspects such as the rules governing significant figures, common mistakes to avoid, and practical examples to solidify your understanding. Whether you're a student seeking to improve your grades or a professional looking to refine your skills, this article will provide you with the tools necessary to master the art of adding significant figures. Let us embark on this journey to enhance our mathematical prowess!
What Are Significant Figures?
Before we dive into adding significant figures, it's crucial to understand what they are. Significant figures, or significant digits, are the digits that carry meaning contributing to their precision. This includes:
- All non-zero digits (e.g., 1, 2, 3)
- Any zeros between significant digits (e.g., 105 has three significant figures)
- Trailing zeros in the decimal portion (e.g., 0.500 has three significant figures)
Why Are Significant Figures Important?
Significant figures play a vital role in scientific and mathematical calculations because they help convey the precision of a measurement. Here are a few reasons why they are important:
- They ensure that the results of calculations are reported with the appropriate level of accuracy.
- They help in avoiding overconfidence in the precision of measurements.
- They maintain consistency in data reporting across various scientific disciplines.
How Do You Add Significant Figures?
When adding numbers that contain significant figures, the following rules apply:
- Identify the numbers you are adding and their respective decimal places.
- Perform the addition as you normally would.
- Determine the number of decimal places in the number with the least decimal places.
- Round the final result to the same number of decimal places as identified in the previous step.
What Are Common Mistakes When Adding Significant Figures?
Even the most experienced individuals can make mistakes when adding significant figures. Here are some common pitfalls to watch out for:
- Neglecting to count trailing zeros correctly.
- Forgetting to round the final answer to the correct number of decimal places.
- Confusing significant figures with decimal places in multiplication or division.
Can You Provide Examples of Adding Significant Figures?
Sure! Here are a couple of examples to illustrate the process:
Example 1: Add 12.11 and 0.3.
- 12.11 has two decimal places.
- 0.3 has one decimal place.
- The answer is 12.41, rounded to one decimal place, resulting in 12.4.
Example 2: Add 5.678 and 2.1.
- 5.678 has three decimal places.
- 2.1 has one decimal place.
- The answer is 7.778, rounded to one decimal place, resulting in 7.8.
What Are Some Tips for Practicing Adding Significant Figures?
To become proficient in adding significant figures, consider the following tips:
- Practice with various examples to build confidence.
- Use online calculators that can help check your work.
- Engage in study groups to discuss common challenges.
How Can Adding Significant Figures Impact Real-World Scenarios?
In fields such as engineering, medicine, and environmental science, the accuracy of calculations can have significant consequences. Here are a few examples of how adding significant figures impacts real-world scenarios:
- In engineering, a small error in measurements can lead to structural failures.
- In medicine, accurate dosages are crucial for patient safety.
- In environmental science, precise measurements are needed to assess pollution levels.
Conclusion: Why Mastering Adding Significant Figures Matters?
Mastering the art of adding significant figures is not just an academic exercise; it's a fundamental skill that has far-reaching implications. Understanding how to properly add significant figures ensures that your calculations are accurate and trustworthy, whether in the classroom or in a professional setting. As you practice and refine your skills, you'll find that adding significant figures becomes second nature, allowing you to approach complex problems with ease and confidence. Embrace the challenge, and let your mathematical journey continue!
Article Recommendations
- Meet Accomplished Leader Jennifer Grant
- Vegamoviestoo The Ultimate Movie Streaming Destination
- The Ultimate Guide To Leslie Easterbrook A Hollywood Icon